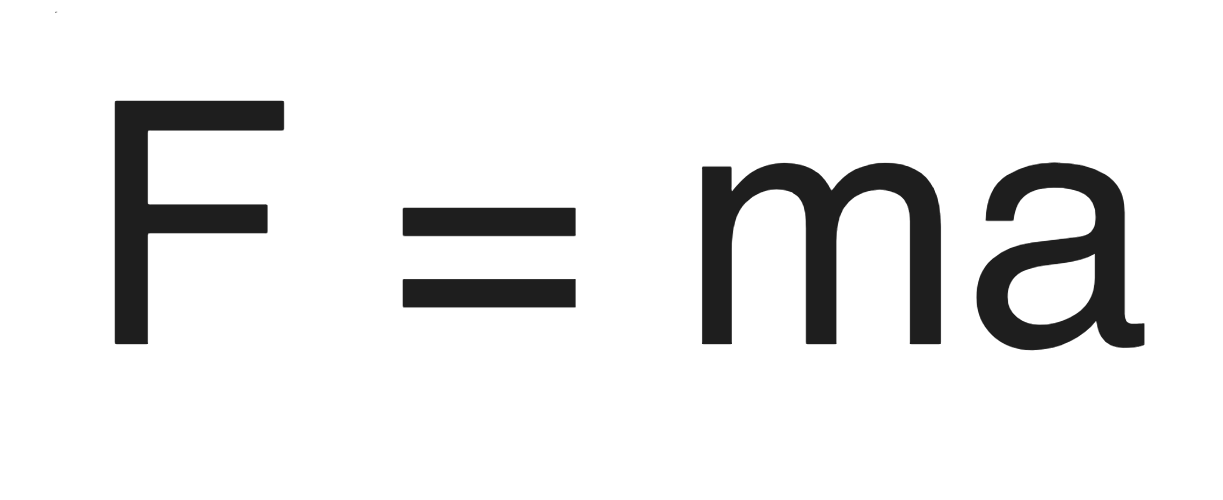
Understanding Newton's Second Law of Motion

Newton's Second Law of Motion, an important concept in physics, builds upon the foundation laid by his first law. While the first law explains the behavior of objects to remain at rest or in motion unless acted upon, the second law dives deeper into how objects actually move when a force is applied to them.

Newton's Second law states: "F = m * a"

The Essence of Newton's Second Law

Imagine pushing a ball along the ground. Newton's Second Law tells us that the ball's acceleration, or how fast it speeds up or slows down, depends on both the force applied to it and its mass. Simply put, the greater the force you apply to the ball, the faster it will accelerate. However, if the ball is heavier (has more mass), it will be harder to accelerate even with the same force applied.

Mathematically, this law is often expressed as F = ma, where F represents the force applied to an object, m stands for its mass, and a denotes the resulting acceleration. It highlights the direct relationship between force, mass, and acceleration: the larger the force applied to an object, the greater the acceleration it experiences, while a heavier object needs more force to accelerate at the same rate as a lighter one.

Significance of Understanding Newton's Second Law

This law holds a lot of importance in various aspects of our lives. For instance, when playing sports like kicking a soccer ball or swinging a bat, the force you apply determines how fast the ball moves or how far the bat can hit it. In engineering, understanding this law is crucial for designing structures, vehicles, and even for calculating how rockets escape Earth's gravity to reach space.

Conclusion

Newton's Second Law is like a guiding compass in understanding how force, mass, and acceleration interact. By comprehending this law, we gain insights into how objects respond to external forces and how these interactions shape the world around us. From simple activities in our daily lives to complex scientific achievements, this law is fundamental in understanding the way things move in our universe.