Today, we’re going to be talk about instantaneous velocity and a visual approach connecting displacement and velocity. 

Instantaneous velocity is mind-boggling. In literary terms, this is an oxymoron, a phrase made by two contradicting words. Instantaneous velocity is best understood as the average velocity over an infinitely small range of time. Remember how in the last episode, we said that:

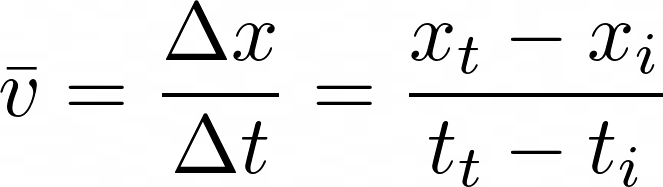
Well, the instantaneous velocity v would be ∆x over ∆t as ∆t approaches 0, denoted by:

Here, dx over dt is actually a calculus concept, but the core definition is the value ∆x over ∆t, evaluated when ∆t approaches 0.

A Visual Approach

Suppose you can graph an objects location to time graph (x-t graph).

The average velocity between two points A and B is simply the slope of the line connecting it. If we can extend this analogy, then it follows that the instantaneous velocity at a point A is the slope of the line tangent to the graph at A.

This is how you can derive velocity from displacement.

You can deduce displacement from instantaneous velocity as well.

The displacement between two times A and B is the area between the graph and the horizontal axis between A and B. There are multiple sources as to why it works, but intuitively the area can be split into infinitely many rectangles each simulating the displacement between two very near times.

As an exercise, try to apply this to constant acceleration motion. 

You can also find more videos on our YouTube, join our Discord for a helpful community, and check out our courses for more help!

Happy learning!